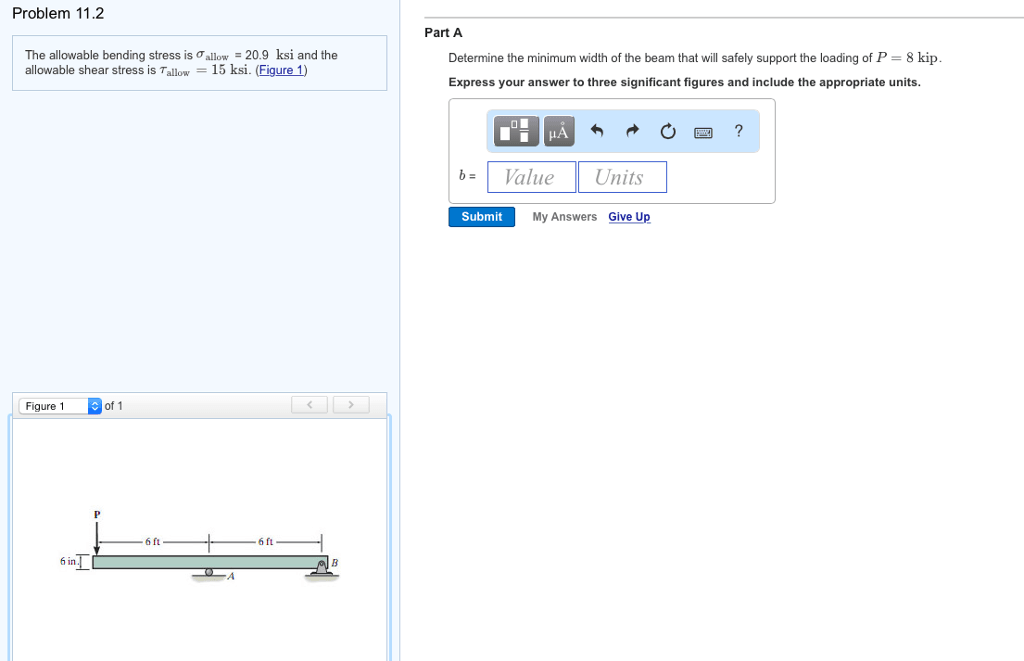
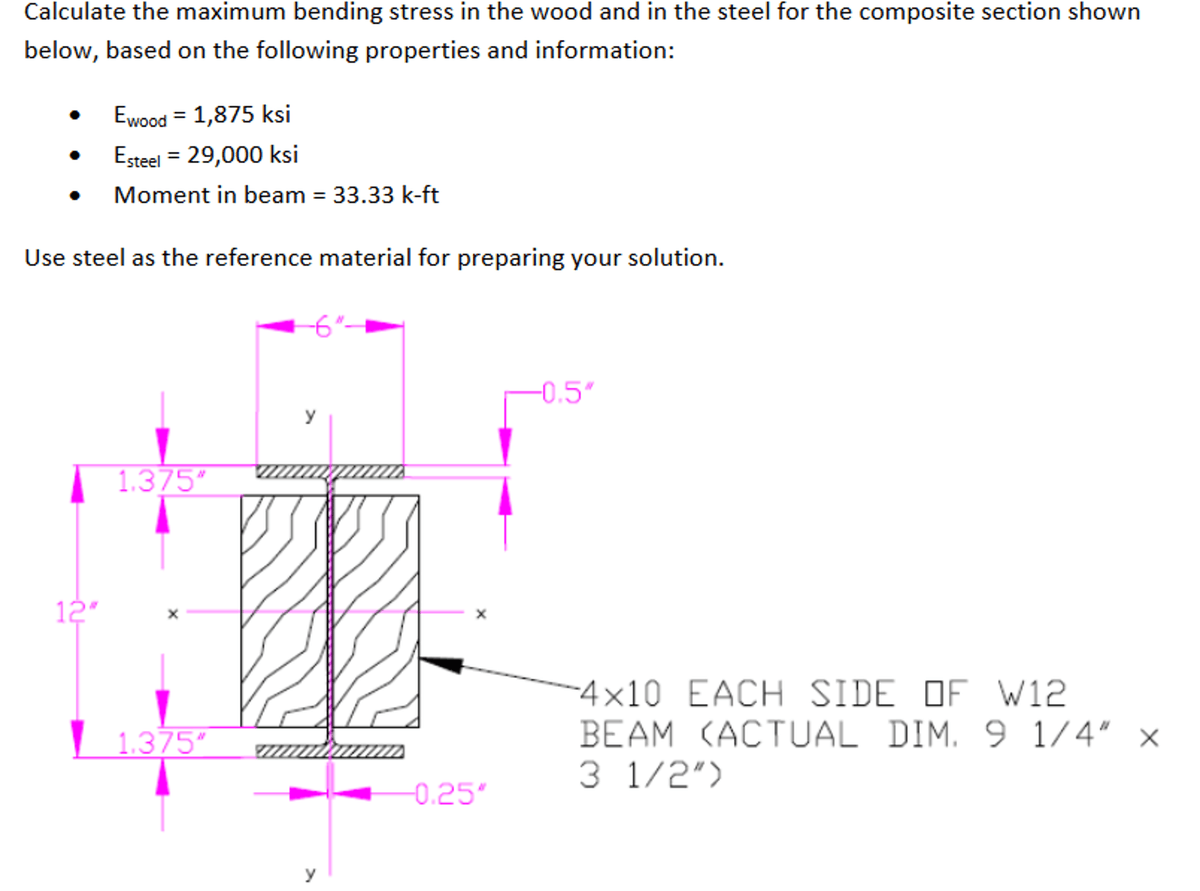
This material is based upon work supported by the National Science Foundation under Grant No. The stress is a function of the applied moment and second moment of area relative to the axis the moment is about. A plane running through the centroid forms the neutral axis – there is no stress or strain along the neutral axis. Both the stress and strain vary along the cross section of the beam, with one surface in tension and the other in compression.
Finally, we learned about normal stress from bending a beam. These diagrams will be essential for determining the maximum shear force and bending moment along a complexly loaded beam, which in turn will be needed to calculate stresses and predict failure. We reexamined the concept of shear and moment diagrams from statics. We learned how to calculate the second moment of area in Cartesian and polar coordinates, and we learned how the parallel axis theorem allows us to the second moment of area relative to an object's centroid – this is useful for splitting a complex cross section into multiple simple shapes and combining them together.
From the first moment of area of a cross section we can calculate the centroid. We learned about moments of area and shear-moment diagrams in this lesson.